Background and Credit
This work was started by Yogesh Mahajan as part of his MTP. He reimagined Nechma's implementation and created a basic working system on FPGA. This page is a development of these ideas keeping scalability in mind.
Motivation and Approach
Motivation
The LU decomposition of sparse matrices is a crucial step in solving
systems of linear equations which are found in a wide range of scientific
applications. However, extracting parallelism is challenging as it is
dependent on the sparsity pattern of the instance. In recent years there has
been a lot of interest in exploiting the inherent parallelism in FPGAs to
accelerate sparse LU decomposition. In domains like circuit simulation, the
fact that the sparsity pattern of the matrix does not change across iterations
can be exploited to build a compute engine optimized for a particular sparsity
pattern.
The Approach
This work exploits the fact that in applications like circuit simulations,
the sparsity of the matrix depends on the topology of the network which does
not change from iteration. This fact is already exploited by mathematical
libraries like KLU. Here we aim to exploit the known sparsity pattern to
statically schedule hardware which extracts fine-grained parallelism.
The Flow

The flow
- Pre-processing
- This step prepares the matrices by permuting the matrix to minimise
the fill-ins. The Approximate Minimum Degree ordering is applied to
pre-order the symmetric sparse matrix prior to numerical factorization.
- Symbolic Analysis
- Here we determine the set of non-zero locations in solving the lower
triangular system Ljx = b, where Lj is a unit
lower-triangular matrix representing only the first (j-1)columns. More
details in section 3.4 of Yogesh's thesis.
- Extract fine-grain parallelism
- Construct a DAG at the finest granularity of single MAC and DIV
operations to execute the steps for LU decomposition. The idea is to
extract parallelism at the lowest level by exposing an array of pipelined
MAC and DIV processing elements to operands which are stored in local
memory (BRAM).
The System
The Hardware
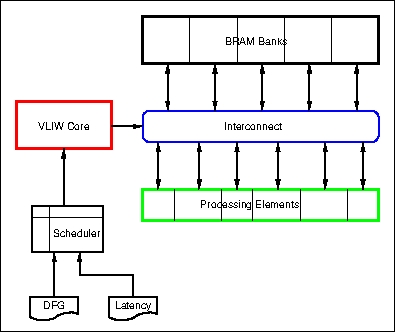
The hardware consists of banks of BRAMs connected to a bank of processing
elements via full-connected interconnect. The BRAMs are dual-ported and double
clocked converting them to quad-port BRAMs. The two processing elements for
the LU factorization are the MAC and the DIV functions. Both of these have
been created by reusing Xilinx IP. An instruction register serves the selects
to the interconnect muxes which routes the operands from the BRAMs to the
processing elements and routes the outputs to the BRAMs.
The Scheduler (Software)
In order to keep the hardware simple while still allowing the extraction of
fine-grain parallelism, the hardware does not support dynamic scheduling. As a
result, the scheduling algorithm has to generate an execution schedule which
takes into account the latencies of the processing elements, intrconnect and
BRAMs. In this implementation we have implemented an As Soon As Possible
(ASAP) scheduler.
Results
Results including comparisons with Nechma's work is available in chapter 8 of
Yogesh's thesis, along with how performance changes with number of PEs, number
of BRAMs, number of BRAM ports and PE latency.

