Mathematical ingredients:

 

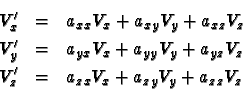
We assume the reader is familiar with the notion of fields as used in physics. For example temperature as a function of position, or the velocity field in a streamline fluid flow. Another well known example is the electromagnetic field. All of these can be thought of as scalar or vector fields in Newtonian space and time. Vector nature of a field means that if the coordinate axes, (physically speaking the frame of reference) are rotated, the values of the three components at each point change in a prescribed manner. If V_x, V_y, V_z are the components of vector V in the old frame and the corresponding components in the new frame are denoted by V_x' etc. then

$$\begin{eqnarray*}V_{x}' & = & a_{xx}V_{x}+a_{xy}V_{y}+a_{xz}V_{z}\\ V_{y}' & = ... ...+a_{yz}V_{z}\\ V_{z}' & = & a_{zx}V_{x}+a_{zy}V_{y}+a_{zz}V_{z} \end{eqnarray*}$$

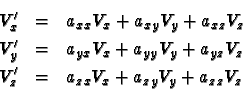
Here a_xx, a_xy, etc. are parameters relating the new and old reference axes. The main points to remember are that the relations are linear (i.e., do not contain terms quadratic or of other powers in the various components) and that it relates the components at the same physical point. The latter property is called locality.

If we are in the domain of Special Relativity, we have to allow for rotations as well as velocity ``boosts", i.e., a change to a frame moving with constant speed relative to the old one. The vectors will now be four-vectors, and hence will also possess a time-like component. In this case too, the relationship between old and new components is linear and local.