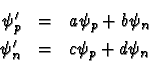Symmetries:

 

Consider an equilateral triangle. Let a particular way of placing it,

  

Figure 1: Example of a symmetry operation on a triangle

as in part (a) of fig 1, correspond to some physical situation. If the triangle is now rotated by 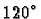as in part (b), there is no discernible change in the situation. If the triangle is a good representation of the physics, the physical situation will be unchanged under this transformation.

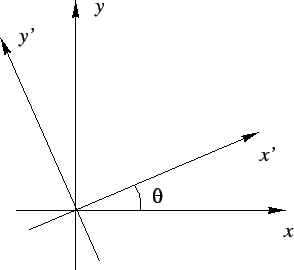
The equivalence to real physics is that instead of a triangle, we have vector fields. Physics is supposed to remain unchanged under rotations or Lorenz transformation of frames of reference. Fig. 2 shows two choices of co-ordinates, with the x'-y' inclined at 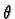with respect to the original x-y system. The components of a given vector field change under such transformations but not the physical answer calculated from them. Such operation are called symmetry operations.

  

Figure 2: Choosing new co-ordinate axes rotated with respect to a given set. Such operations are symmetries of Physics.

In 1930's the notion of such symmetry was extended by Heisenberg in a very profound way. It is known that the strong nuclear force does not distinguish between the proton and the neutron, or separately, among the three pions , and 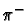. He proposed that the strong nuclear force is unchanged even if the physical state is an arbitrary, though linear. admixture of the proton and the neutron. In Quantum Mechanics, the physical state of a system is described by a complex wavefunction denoted . 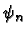Heisenberg's proposal was that instead of using (for proton) and (for neutrons), we could define new wavefunctions 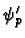and given by

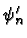$$\begin{eqnarray*}\psi _{p}' & = & a\psi _{p}+b\psi _{n}\\ \psi _{n}' & = & c\psi _{p}+d\psi _{n} \end{eqnarray*}$$

and the physics would remain unchanged. Here the 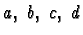are complex numbers satisfying some constraints. The relations above can be thought of as a complex rotation, an abstract generalisation of the case of real vectors discussed in section 2.1. This rotation, called an isospin rotation is a symmetry (although approximate) of the strong nuclear force.