Gauge invariance of Electromagnetism:

In the 1920's Hermann Weyl pointed out a symmetry of Electromagnetism that was different in technical detail but very similar in spirit to the Principle of General Covariance. This symmetry he called the Gauge Principle.

Suppose we write the Maxwell Equations, not in terms of Eand B fields, but in terms of the four-vector potential field 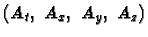. It can then be shown that Maxwell's equations are unchanged if we choose a different vector field such that

$$\begin{eqnarray*}A_{t}' & = & A_{t}+{df\over dt}\\ A_{x}' & = & A_{x}+{df\over dx} \end{eqnarray*}$$

etc., where f is a function of space as well as time, t. This is like the triangle we had in sec. 2.2. We need an equilateral triangle, but somehow the Physics does not depend on which corner is which. Here we need a four vector field but if the components are all changed in the specific form given above, it does not affect the Physics. It is important to note that the change is not at all like a Lorentz transformation of inertial reference axes. We have an independent change in components at each point in space-time. This is because f is a function of space and time.

Now this situation is quite similar to the case of General Covariance, where invariance under arbitrary coordinate changes amounted to independent Lorentz transformations at each point. Furthermore, as in the case of General Covariance this invariance of Electromagnetism also helps to fix the interaction of electromagnetic fields with charged matter. We discuss this next. In Quantum Mechanics, matter is described by a wavefunction . We now insist on making the change

$$\psi '({\textbf {x}},t)=e^{if({\textbf {x}},t)}\psi ({\textbf {x}},t)$$

with the same f as in the preceding equation. Thus the phase of the wavefunction is simultaneously changed in a space-time dependent manner. The law of interaction of charges and electromagnetic fields is invariant under this simultaneous change. This Principle has now been established to a great level of accuracy. It also reproduces correctly the interaction of classical (macroscopic) currents and charges with electromagnetic fields.