Consensus over Pseudo-undirected Graphs
In multiagent systems, some agents will have larger initial state values, while others may have smaller initial state values. The distributed leaderless framework with undirected graphs can only ensure a consensus value which is at the average of the agents' initial states. Sometimes, this may emerge as a restrictive requirement. One way to tackle this is to adopt a leader-follower scheme, and providing a wide range of arbitrary reference values to the leader. That said, the situation becomes over-dependent on a single agent. In either case, some agents do not affect the consensus value. We focus on a fully distributed cooperative behavior that also guarantees interception at values which are not at the average of the agents' initial states. With the proposed nature of interaction, each agent has a stake in the consensus value. Physical constraints on actuators, such as bounded lateral acceleration of vehicles, are also respected when agents are connected over the proposed pseudo-undirected graph.
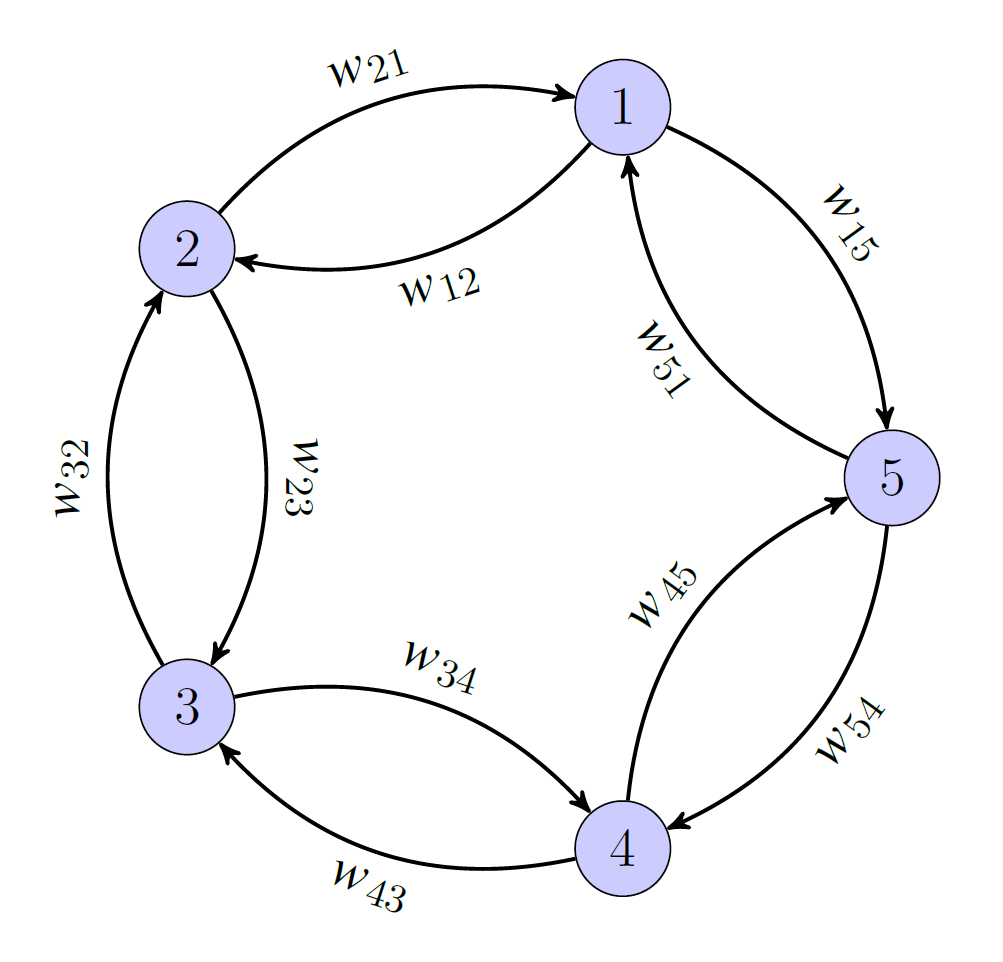
We also analyze the extent to which a single edge weight can be (negatively) perturbed without agents losing consensus. A direct application of this work can be seen in cooperative simultaneous interception of a target when the common time of interception is desired larger than the largest time-to-go in the swarm.
